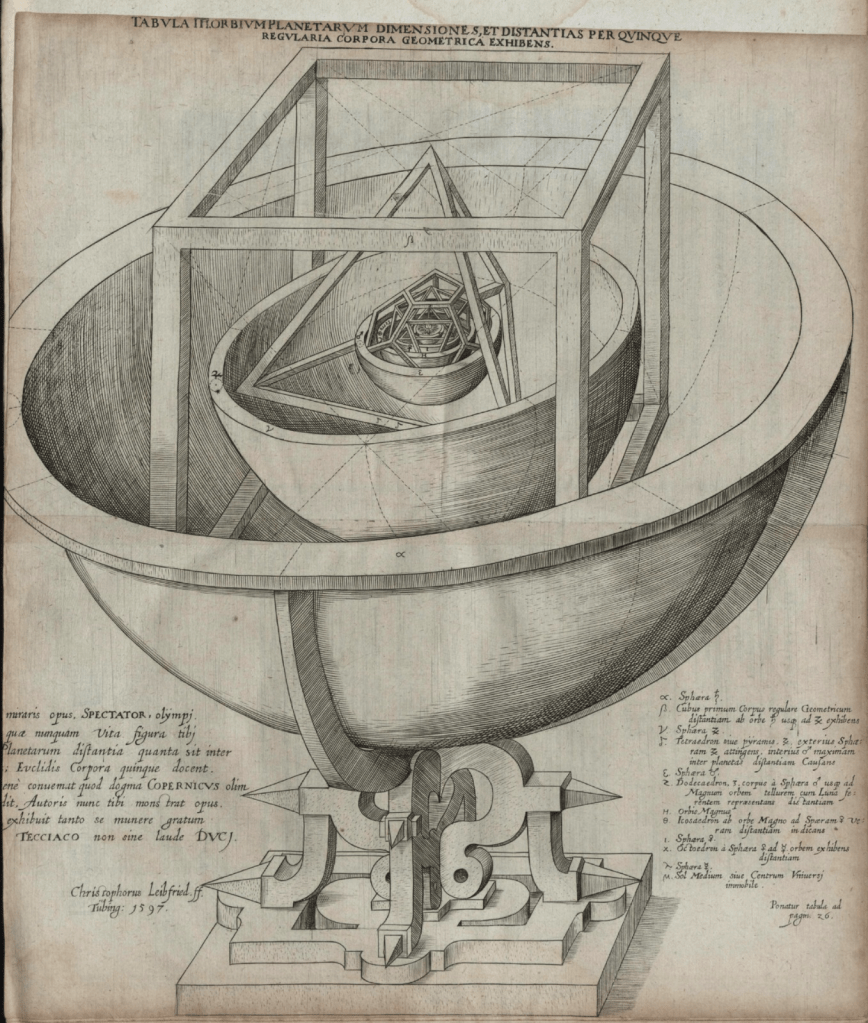
Apparentemente è una domanda senza fine, senza direzione, un dubbio che come un sasso viene lasciato cadere nel pozzo dell’ignoto per vedere quanto sia profondo, bambinesco gioco per le pretese di conoscenza dell’iconoclasta che vuole sfidare le Colonne d’Ercole, è interessante notare come questo sia stato un quesito dominante nelle menti dei pensatori in quelle antiche terre dove non si era sviluppata una dottrina cosmogonica o eziologica troppo prominente per fermare i lumi della filosofia. Questo articolo si propone come lavoro di ricerca spaziante vari campi per delineare un’evoluzione concreta del pensiero occidentale sull’argomento, rapportandolo alle più moderne e accreditabili teorie scientifiche.

---

I: La Sfera di Parmenide

---

II: Il Paradiso Dantesco

Anche se il nome di Parmenide mancò totalmente di menzioni per un periodo ingiusto relativamente alla grandiosità del suo intelletto, quell’intuizione primordiale e archetipa della sfera come geometria trascendentale e perfetta della natura permeò il collettivo del sapere da Aristotele fino a Copernico, radicandosi nella filosofia, nelle scienze, nella teologia cristiana, nelle arti ermetico-esoteriche, e nell’alchimia: è il sistema geocentrico aristotelico-tolemaico, con l’universo descritto come stratificazione di sfere concentriche, con le stelle fisse, o Primo Mobile, come involucro finale.

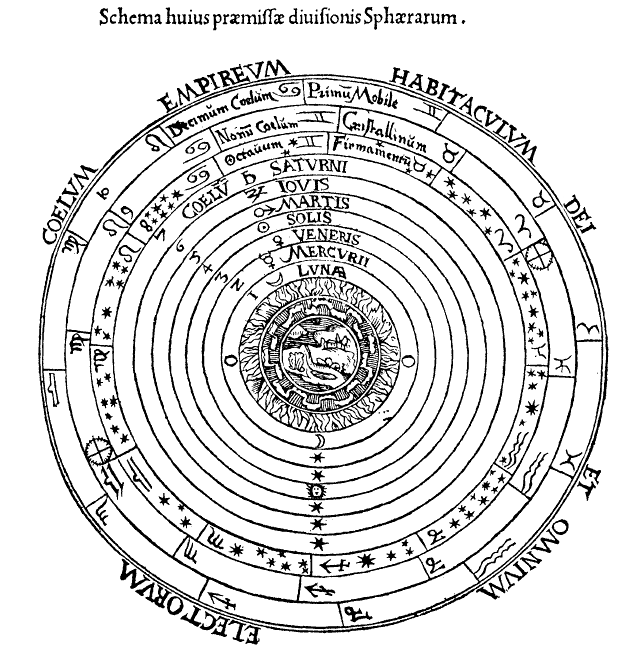
E’ importantissimo notare come questa non sia stata per niente una struttura univoca: nell’analisi dei versi del Paradiso della Divina Commedia, di fatto, ci viene presentata una cosmografia completamente eterodossa rispetto all’era di Dante, con tantissimi paralleli alla matematica moderna ma nessun corrispettivo anteriore alla stesura della Commedia.
Partendo dal modello aristotelico-tolemaico, il poeta ripercorre tutte le sfere celesti arrivando nel corso del canto XXII a vederne, da dietro, quasi tutte racchiuse dentro se stesse, dalla costellazione dei gemelli; egli descrive con la sequente terzina, in questo frangente, la seguente scena:

Col viso ritornai per tutte quante
le sette spere, e vidi questo globo
tal, ch’io sorrisi del suo vil sembiante;

“Paradiso”, canto XXII, vv. 133-135

dandoci la prova che riesca a vedere di concreto tutte le sfere da lontano come un singolo globo.
La vera astrazione, però, avviene alcuni canti dopo, nel XXVIII, in cui al lettore viene detto:

distante intorno al punto un cerchio d’igne

si girava sì ratto, ch’avria vinto
quel moto che più tosto il mondo cigne;

e questo era d’un altro circumcinto,
e quel dal terzo, e ‘l terzo poi dal quarto,
dal quinto il quarto, e poi dal sesto il quinto.

Sopra seguiva il settimo sì sparto
già di larghezza, che ‘l messo di Iuno
intero a contenerlo sarebbe arto.

Così l’ottavo e ‘l nono; e chiascheduno
più tardo si movea, secondo ch’era
in numero distante più da l’uno;

e quello avea la fiamma più sincera
cui men distava la favilla pura,
credo, però che più di lei s’invera.”La donna mia, che mi vedëa in cura
forte sospeso, disse: “Da quel punto
depende il cielo e tutta la natura.”

“Paradiso”, canto XXVII, vv. 25-42

Dante, dal Primo Mobile, riesce a vedere tutte le nove sfere dei cori angelici intorno all’Empireo, ma noi sappiamo che deve necessariamente avere un panorama chiaro delle sfere celesti intorno alla Terra: com’è possibile che riesca a vederle entrambe?
“Questa è bensì una domanda banale”, penserebbe un qualsiasi lettore, difatti basta che i cerchi siano connessi, o tangenti, per un preciso punto in comune che faccia da varco, come nell’esempio grafico sotto citato:

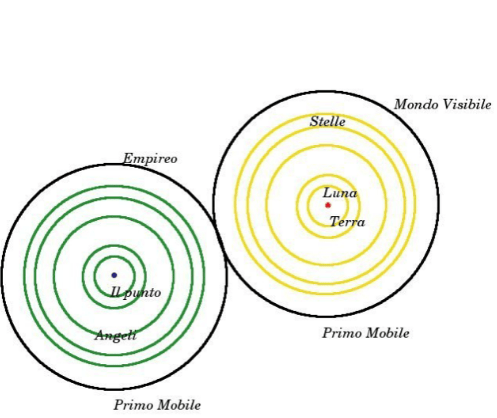
o in tre dimensioni, come sarebbe meglio:

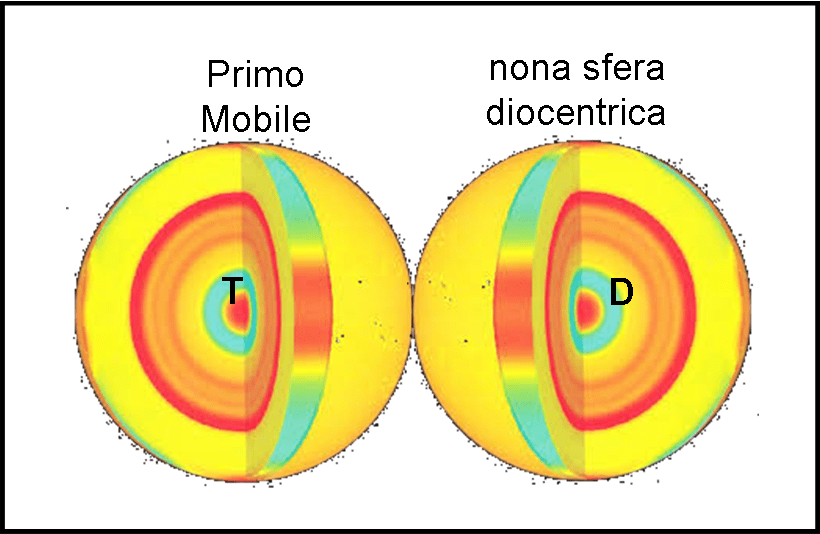
ahimé, Dante era una mente troppo eccentrica per cadere in queste banalità, e sembra ci abbia preparato dei versi appositamente per sfatare questa ipotesi!

Le parti sue vivissime ed eccelse
sì uniforme son, ch’i’ non so dire
qual Beatrice per loco mi scelse.

“Paradiso”, canto XVII, vv. 100-102

Dante fa esplicita menzione che egli si trovi insieme a Beatrice in un punto totalmente non precisato e omologo agli altri, e che il Primo Mobile sia di conseguenza assolutamente omogeneo, senza alcuna coordinata speciale che connetta le due sfere!
Ma allora, in che modo è coerente l’apparentemente contraddittoria struttura del Paradiso?
In nostro aiuto, interviene la geometria, un po’ di carta, forbici, colla, e normale capacità manuale.
Per convenzione (e limiti mentali), immaginiamo il Paradiso come strettamente bidimensionale, con semplici cerchi al posto di sfere complete: immaginiamo, quindi, al posto di tracciare i cerchi celesti della Terra e dell’Empireo su foglio piatto, segnamoli sulle due metà di una sfera di carta che abbiamo tagliato con le forbici, con i confini che simbolizzano il Primo Mobile:

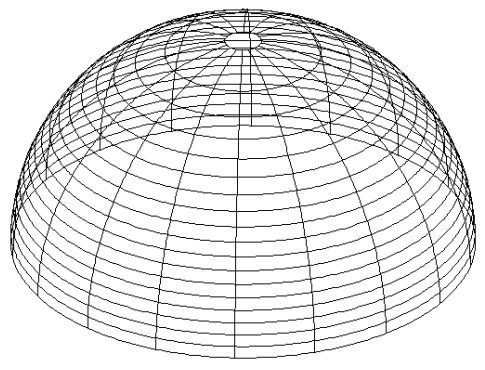
un polo rappresenta la Terra, l’altro Dio come ce lo descrive Dante, e scendendo troviamo tutte i corrispettivi “cerchi”; adesso prendiamo un po’ di colla e mettiamola su entrambe le estremità, e perciò, attacchiamo!

Tutti i punti del Primo Mobile sono ora collegati e perfettamente omologhi, permettendo però di vedere entrambi i sistemi di “cerchi” concentrici per ciascuno di essi!
Dante ora, però, è un essere bidimensionale messo sulla superficie di una sfera, anche detta 2-sfera, dove l’indice iniziale rappresenta il numero di dimensione della superficie/contorno (per fare un esempio, il contorno di un cerchio, la sua circonferenza, potrebbe essere considerata in termini matematici 1-sfera, essendo di dimensione 1, ovvero una linea); come facciamo a farlo diventare un essere umano in carne ed ossa?
La soluzione più intuitiva sarebbe quella di semplicemente scalare di 1 le dimensioni, ma non è affatto agevole come esercizio di immaginazione: il Sommo Poeta ora si troverebbe sì in dei globi veri e propri, ma questi globi, a loro volta, dove si trovano?
E’ necessario immaginare un oggetto totalmente trascendente, che come superficie possa avere un intero spazio tridimensionale vero e proprio: sto intendendo un’ipotetica 3-sfera, un globo in quattro dimensioni, anche detta ipersfera.

Questa figura, di primo impatto grottesca a nostalgicamente lovecraftiana, è la proiezione della fibrazione di Hopf, una simbolica rappresentazione in (circa) tre dimensioni di un’ipersfera usando cerchi e sezioni di sfera, che su un piano assume ai nostri occhi la forma di un toro (figura della topologia simile ad una ciambella):

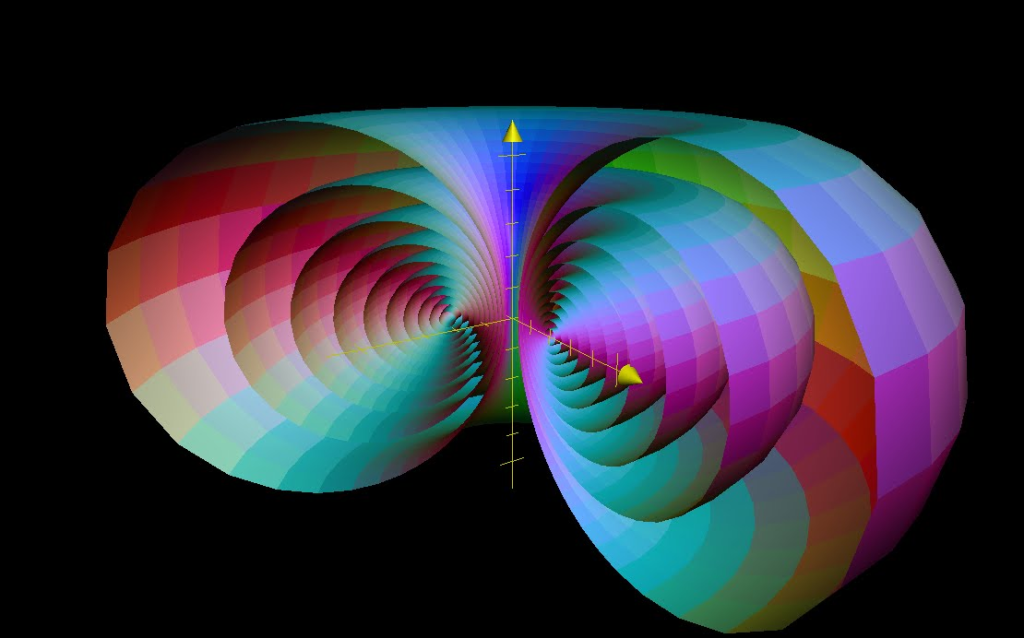
Usare tutte queste rappresentazioni simboliche di oggetti geometrici quadridimensionali provvedendo testi esplicativi mi sembra un compito di difficoltà ragguardevole, soprattutto per l’aspetto relativo ad essere consoni ad un semplice giornalino scolastico, e ho intenzione di rimanere all’iconografia della 2-sfera, benché questi risulti imprecisa.
Comparando le sfere celestiali ai cerchi tracciati sul globo di carta, otteniamo questa come raffigurazione finale:

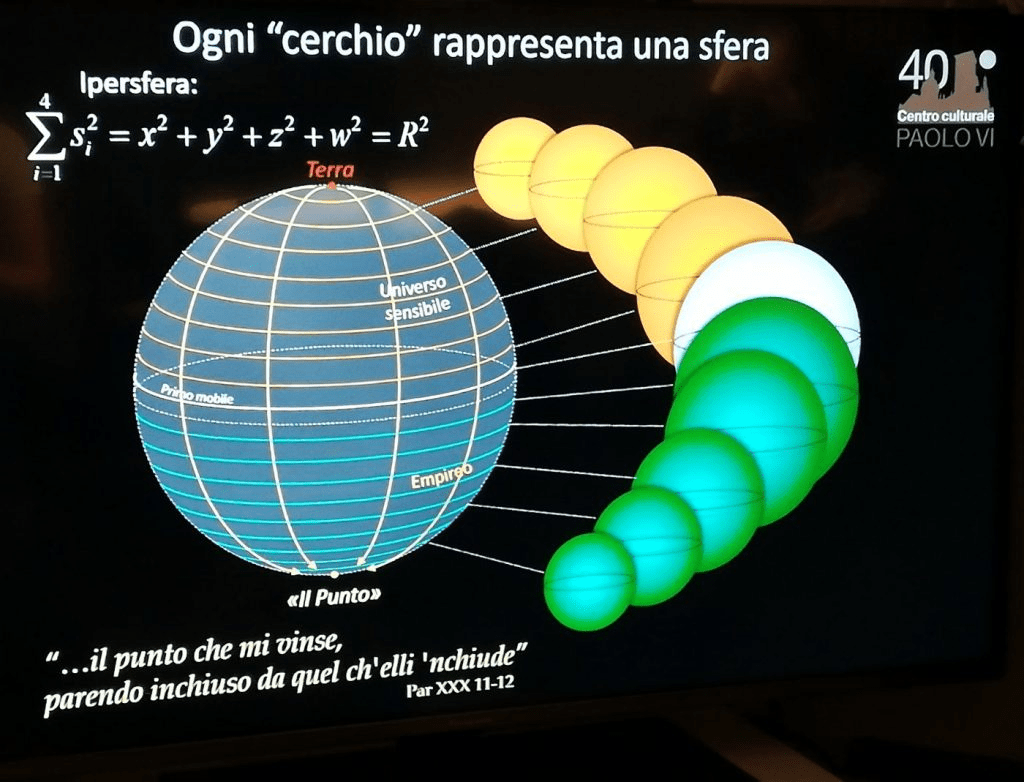
Non sapremo mai se il genio senza eguali di Dante avesse davvero immaginato ciò che noi, con gli strumenti della matematica moderna, chiamiamo 3-sfera, ma sarebbe davvero straordinario come conclusione, dati i numerosi indizi sparsi per i canti del Paradiso.
Per il prossimo capitolo portatevi addietro la conclusione che l’Universo possa essere una 3-sfera, ovvero la superficie tridimensionale di un’ipersfera.

---

III: Che forma ha l’universo?

Ritornando alla nostra analisi storica, ahimé nessuno capì davvero l’importanza di quei sacri versi fino all’epoca moderna, il modello aristotelico-tolemaico prevalse comunque nella sua forma più classica e conosciuta, e anche dopo Galileo e Keplero e l’instaurazione dell’eliocentrismo, l’Universo sarebbe rimasto oltremodo sferico e finito (per gli studenti di filosofia, tenete a mente, e magari a cuore, il nome di Giordano Bruno, uno dei pensatori più incredibili del rinascimento, un vero profeta che per primo avrebbe pensato l’Universo come “infinito”, parola che stava sul punto per essere normalizzata dal nuovo calcolo infinitesimale di Newton e Leibniz, ma che gli è costata la vita per essere stato giudicato come eretico dall’inquisizione!).
Ma, con l’evolversi della fisica, agli inizi del ventesimo secolo, l’allor giovane astrofisico Edwin Hubble, dall’osservatorio di Monte Wilson, in California, scoprì il fenomeno del redshifting delle galassie lontane da noi, ovvero un loro progressivo, ma spaventosamente veloce, allontanamento in tutte le direzioni rispetto alla Via Lattea, percepibile dal graduale spostamento delle loro frequenze elettromagnetiche verso gli infrarossi e le onde a bassa frequenza. La prova dell’universo in espansione aprì nuove strade ai cosmologi di quel tempo, che proprio in risposta al rilevamento del redshifting, pubblicarono delle primissime versioni dell’agognata teoria del Big Bang. Le conseguenze logiche derivate dalla scoperta dell’inflazione cosmica furono molteplici, ma tra queste ricordiamo l’assenza di un centro dell’universo, in quanto esso si sta espandendo in ogni singola direzione rispetto ad ogni singolo punto, e l’assenza di un contorno, poiché non si sta espandendo in un altro spazio ma è lo spazio stesso intrinsecamente ad espandersi (in altre parole, si sta espandendo in se stesso!). Ricordare che il fatto che si stia espandendo non indica necessariamente che sia né finito né infinito, in quanto il modo in cui si sta espandendo (in maniera intrinseca, tramite la modifica oggetti algebrici del modello einsteiniano chiamati “tensori”, una sorta di legenda divina delle proprietà di un dato spazio) è fisicamente possibile sia se l’universo è finito sia se non lo è. Ad un primo impatto per niente salienti, queste nuove deduzioni ci forniscono una conclusione incredibile: l’universo non può avere la forma di area/volume di qualsiasi oggetto geometrico definito, specialmente di una globo, in quanto necessiterebbe di un centro e una superficie esteriore!
In aggiunta a questi due punti, nel 1964, ai Bell Laboratories del New Jersey, dopo le prove del nuovo radioscopio, i fisici Arno Pensias e R. W. Wilson rilevarono come costante interferenza la radiazione cosmica di fondo, luce risalente ai primi periodi di vita dell’universo che, se mappata, rivela un’immagine, sebbene a macchie, omogenea dell’Universo: sia come lo vediamo ora, sia com’è stato, sembra sempre uguale indipendentemente dal luogo dove si guardi, e indipendentemente dalla direzione in cui noi guardiamo!

---

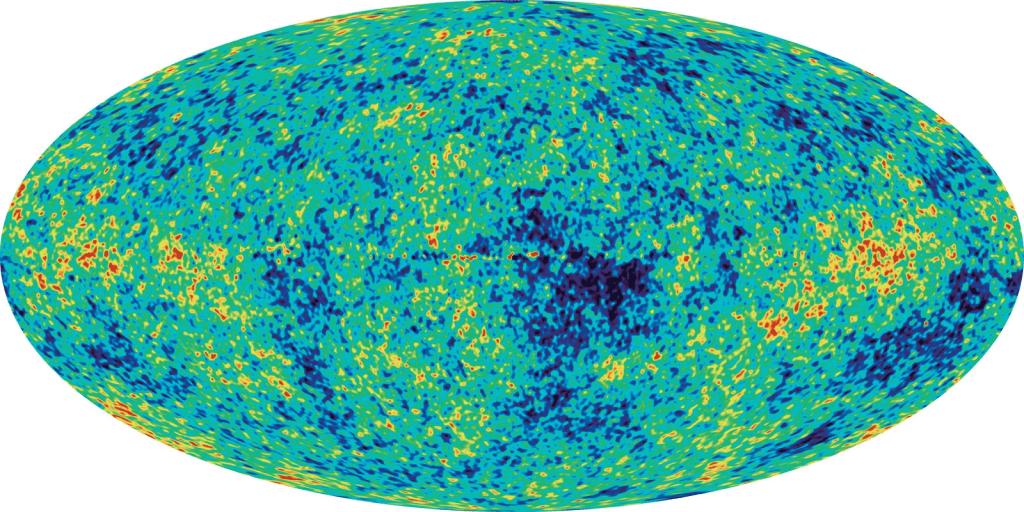
Riassumendo le informazioni a nostra disposizione, come specie umana sappiamo che:

• L’Universo sembra seguire localmente la geometria euclidea a 3 dimensioni, in altre parole che sia tridimensionalmente piatto nell’area osservabile
• E’ omogeneo, sembra uguale ovunque lo si guardi
• Non ha un centro
• Non ha un confine
• Si sta espandendo, indipendentemente dal luogo in cui siamo 
• Non è necessariamente infinito

Dunque, com’è possibile trovare un oggetto geometrico che soddisfi tutte queste proprietà?
Prima di andare alla ricerca di indiziati, è necessario ricordarsi un alquanto ridondante e fastidioso fatto: noi non sappiamo quanto grande sia l’Universo.
Sappiamo benissimo l’ampiezza della sezione di Universo a noi osservabile, ma non abbiamo nessun strumento per asserire di preciso a che percentuale del totale corrisponda, almeno se volessimo mantenere rigore senza approssimazioni.
Anche se localmente per noi l’universo segue la geometria euclidea piana, nella globalità delle sue proprietà potrebbe seguire leggi completamente diverse: potrebbe essere curvo. E oltre alla geometria piana, troviamo quindi ben due modelli che seguono questa curvatura: la geometria ellittica (anche detta sferica), curva positivamente, e la geometria iperbolica, curva negativamente.
Questi modelli condividono un aspetto fondamentale nel capovolgimento del quinto postulato Euclide, riguardante le rette parallele, in quanto, per via della curvatura, dicono come due rette parallele fra loro possano avvicinarsi fino ad incontrarsi o allontanarsi, in opposizione alla geometria piana che ci dice rimangano sempre alla stessa distanza.

---

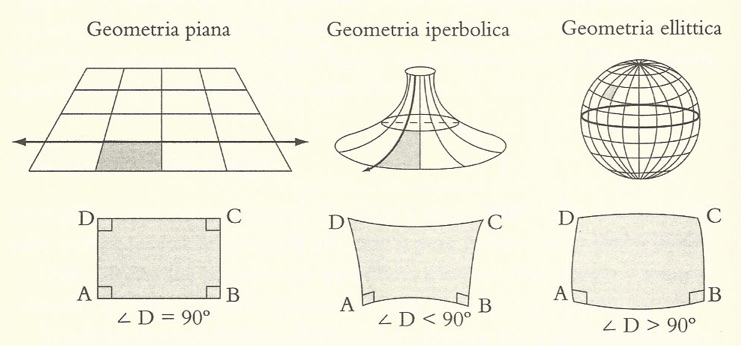
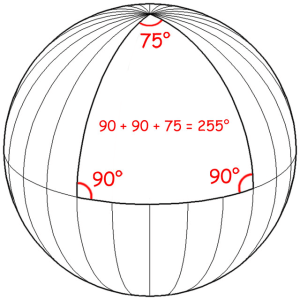
La geometria ellittica è particolarmente utile in quanto modella le regole della superficie delle sfere, ed è importante notare, come per la curvatura positiva, tutti i triangoli in questo spazio presentino la particolare proprietà di avere la somma degli angoli interni sempre maggiori di 180 gradi:

---

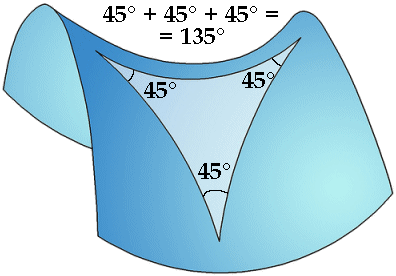
La geometria iperbolica, d’altro canto, non descrive la superficie di un determinato solido, in quanto esistono vari oggetti topologici diversi che rientrano nelle specifiche ma con determinati aspetti variabili, ma è usata generalmente nel calcolo infinitesimale e l’analisi, per le particolarità delle sue funzioni trigonometriche sinh, cosh, e tanh (da leggere: seno iperbolico, coseno iperbolico, tangente iperbolica); presenta altresì la proprietà di permettere triangoli con somma interna degli angoli minore di 180 gradi.

---

Ora, ricapitoliamo brevemente alcune delle caratteristiche salienti dell’oggetto geometrico che stiamo cercando:

• Non ha un centro
• Non ha un confine 
• Non è necessariamente euclideo (almeno globalmente)
• Non è necessariamente finito
• E’ finito

C’è un solo ente che può soddisfare ognuna di queste proprietà: una superficie!

Se siamo ad esempio sulla superficie di una sfera, è vero che possiamo dire che il globo in sé abbia un centro da cui parte il raggio, ma se rimaniamo solo sulla superficie, possiamo dire per concreto che non  ci sia alcuna coordinata centrale, a meno che non scegliamo arbitrariamente due poli; su una sfera possiamo camminare in qualsiasi direzione, senza mai arrivare a un limite, difatti camminando in linea retta ritorneremo dopo un po’ al punto iniziale; inoltre, non importa da quale punto la si veda, la sfera è rimarrà completamente uguale ed omogenea.

Cerchiamo di riproporre la sfera come contendente per essere la forma dell’Universo, scalando di uno le dimensioni: otteniamo una superficie sferica tridimensionale, una 3-sfera, lo stesso solido del Paradiso di Dante!
Dobbiamo tenere a mente, però, che in questo caso non abbiamo più a che fare con alcuna sfera celeste o Empireo, ma che i poli dove erano presenti la Terra e Dio siano uguali agli altri: in sostanza, tutto l’Universo sarebbe Primo Mobile.

La 3-sfera è la superficie ellittica principale che può soddisfare tutte le nostre condizioni, ma vogliamo rimanere nel campo della geometria piana, c’è un solido altrettanto importante con le stesse proprietà sopra elencate: il toro.

Questa particolare figura “a ciambella” condivide ogni aspetto con la sfera pur rimanendo euclideo; facendo una prova, tracciando linee parallele queste rimarranno tali ad una distanza fissa, senza alcuna curvatura positiva o negativa; manca di centro come le altre superfici, e un qualunque oggetto su questo piano, camminando su una retta, ritornerebbe alla posizione iniziale sia passando per il contorno sia per il buco (terminologia specifica della topologia). Vivendo in tre dimensioni, avremmo bisogno di un 3-toro, la superficie tridimensionale di un toro quadridimensionale.

Ci rimangono da affrontare eventuali superfici di solidi quadridimensionali di geometria iperbolica, ma perché non c’è un singolo candidato che rappresenti tutto come nel caso della sfera, tratteremo due oggetti distinti: l’iperboloide e la pseudosfera.

---

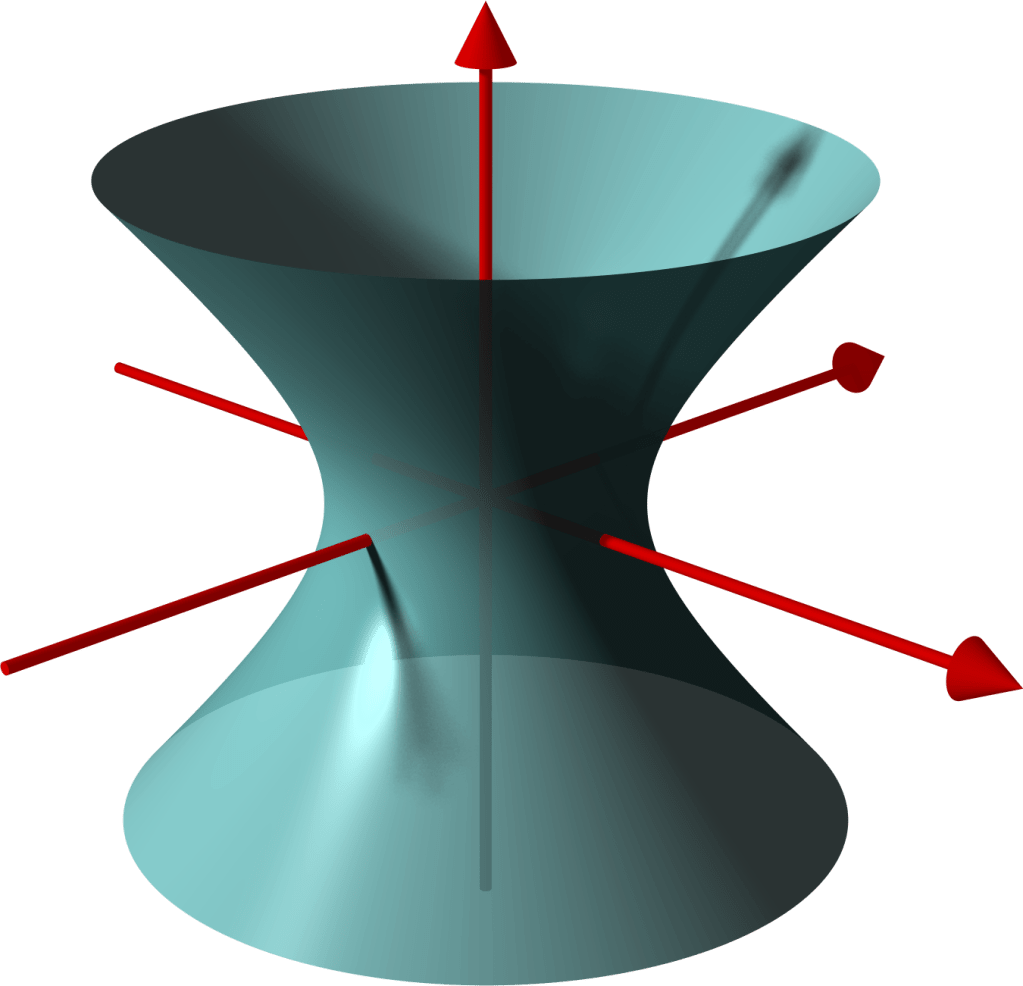
L’iperboloide è una figura nata dalla rotazione del grafico di un’iperbole rispetto ad uno dei suoi assi focali. La sua sezione, la cosiddetta “sella”, è un piano di riferimento molto comune per rappresentare spazi iperbolici:

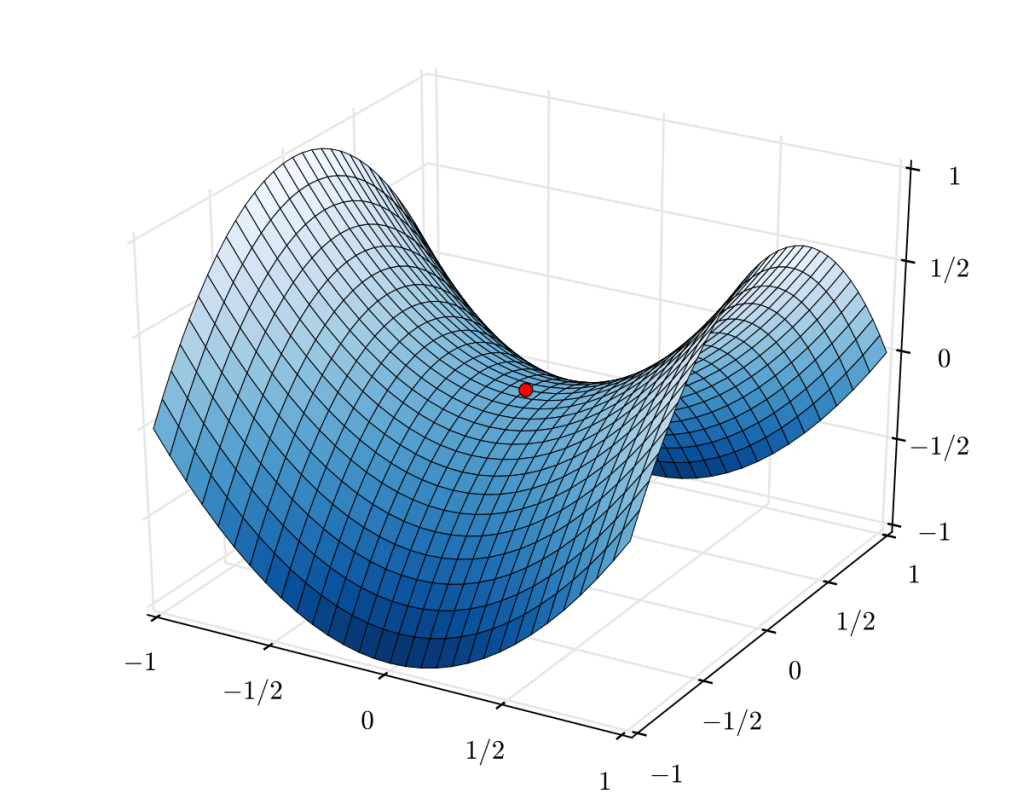
A differenza della sfera e del toro, l’iperboloide, per la sua stessa costruzione può espandersi all’infinito ed avere superficie illimitata; si può provare matematicamente che esso sia omogeneo. Per il nostro universo abbiamo quindi bisogno di un 3-iperboloide, o 3-sella.

---

Rimane dunque la pseudosfera, nata dalla rotazione di uno speciale grafico di funzione detto trattrice:

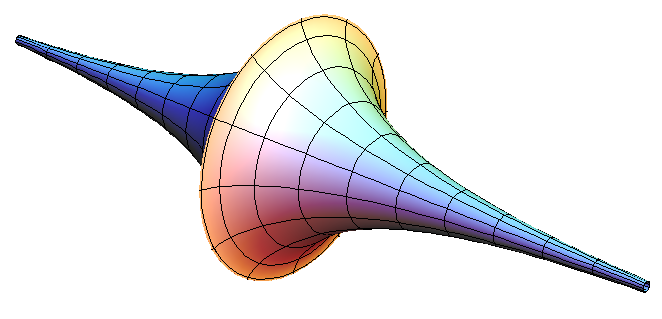
Come l’iperboloide, ha superficie illimitata.

---

Ricapitolando, possiamo costruire la seguente tabella:

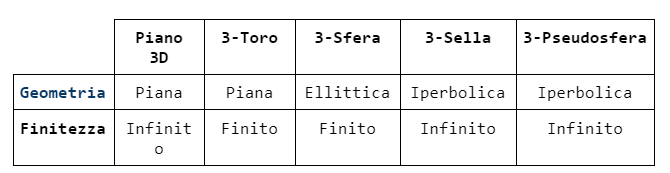
Poiché nell’Universo osservabile non si è mai rilevata alcuna curvatura della luce che non sia mai stata causata dalla gravità, gli spazi di geometria piana hanno sempre avuto un ruolo più importante nella possibile cosmografia dell’universo, mentre i modelli non-euclidei sono stati usati principalmente a fini cosmologici, come rappresentazioni delle possibili sviluppi dell’inflazione rispetto ad una quarta dimensione temporale: sulla 3-Sfera, partendo da un punto come polo simbolizzante il Big Bang, arriveremo all’equatore come massima espansione dell’Universo, con questo che si rimpicciolisce arrivando all’altro polo singolarità (Big Crunch); sull’universo 3-Sella, da un punto nella “valle” l’universo si espanderebbe esponenzialmente all’infinito (Big Rip/Big Freeze).

La teoria dell’Universo 3-Toro ha avuto una lunga e dibattuta storia, soprattutto per le conseguenze che avrebbe: se la luce di un oggetto tornasse sempre indietro per la struttura a ciambella del toro, dovremmo aspettarci di vedere infinite serie di immagini residue di ogni oggetto tagliare lo spazio profondo, e addirittura di osservare nelle rilevazioni la luce della nostra stessa galassia a specchio, come accade nell’effetto visivo dell’infinity mirror:

---

Per i Dantisti speranzosi, sperate che non stiamo rilevando alcuna curvatura positiva dello spazio perché è troppo grande, magari stiamo già vivendo nel Paradiso.